線分交差判定
外積
線分\(\alpha, \beta\)について
\[
\begin{cases}
\overrightarrow{\alpha}: \overrightarrow{AB} \\
\overrightarrow{\beta}: \overrightarrow{CD}
\end{cases}
\]
\(\vec{\alpha}, \vec{\beta}\)について各3ベクトルを考える
\[
\overrightarrow{\alpha}:
\begin{cases}
\overrightarrow{AB} \\
\overrightarrow{AC} \\
\overrightarrow{AD}
\end{cases}\\
\]
\[
\overrightarrow{\beta}:
\begin{cases}
\overrightarrow{CD} \\
\overrightarrow{CA} \\
\overrightarrow{CB}
\end{cases}
\]
上記の各ベクトルを\(\overrightarrow{1}, \overrightarrow{2}, \overrightarrow{3}\)とすると下記より各線分について、他方の線分がベクトルについて左右に位置しているか判定でき、各線分について左右に位置している場合、交差していると判断できる
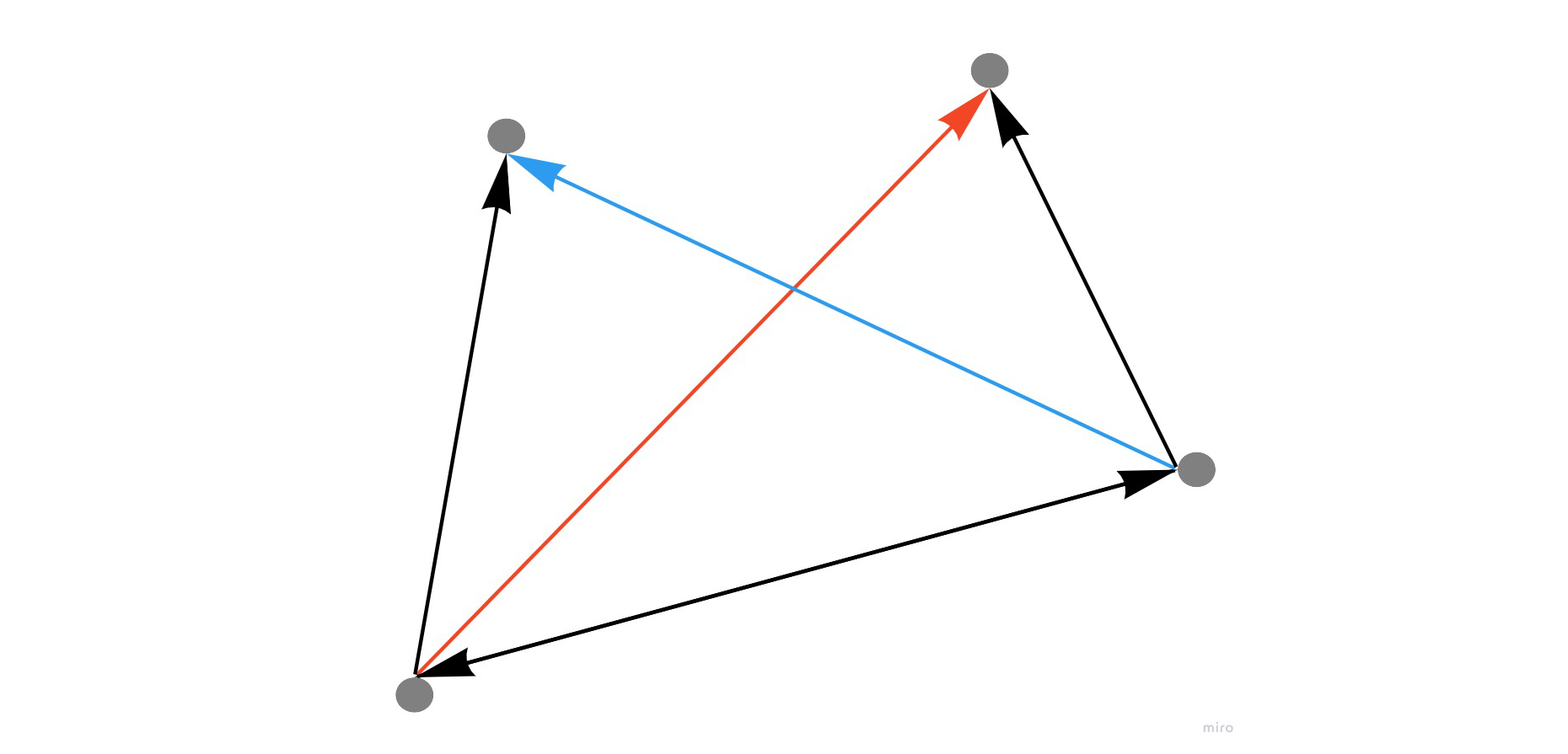
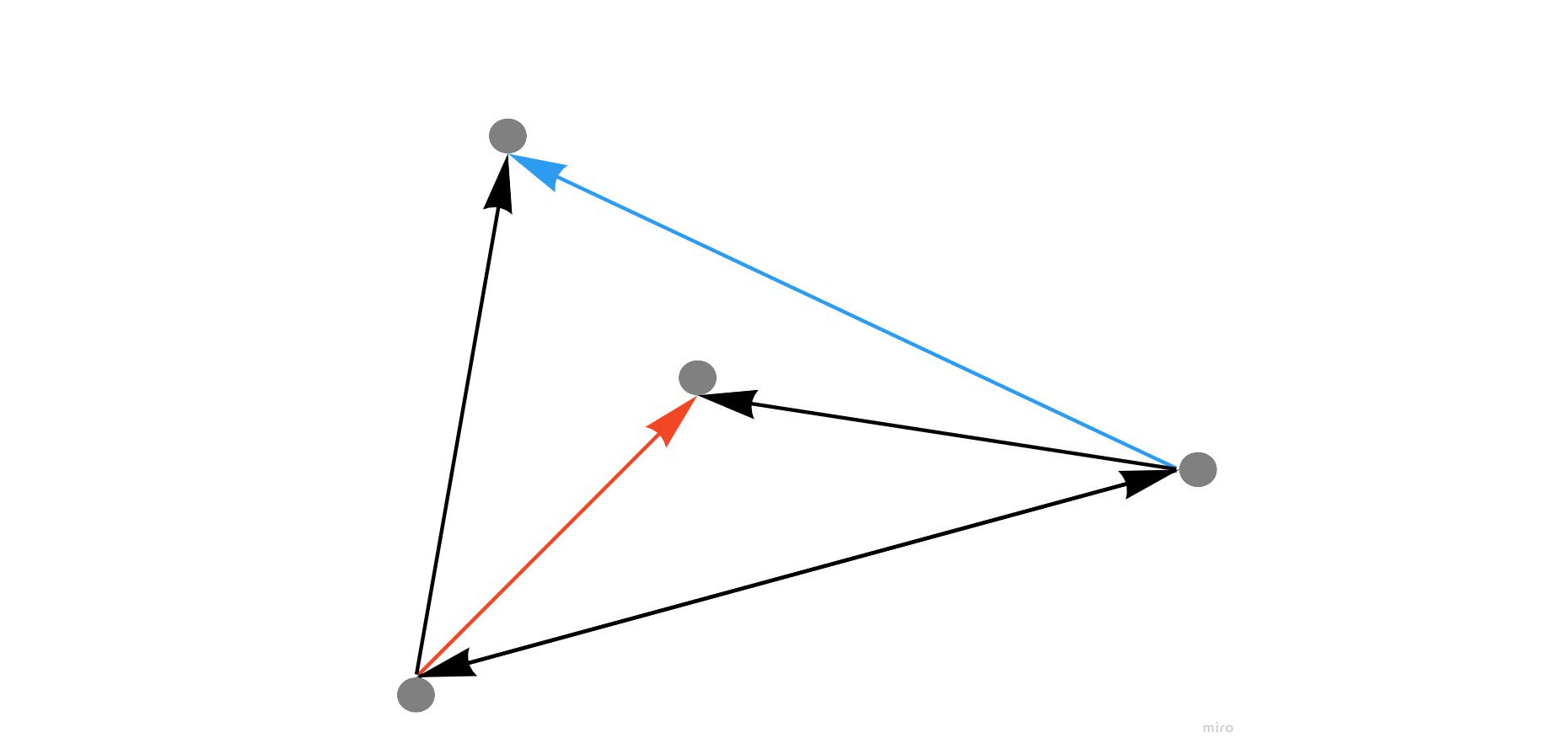
\[
result = (\overrightarrow{1}\times\overrightarrow{2})(\overrightarrow{1}\times\overrightarrow{3})
\]
\[
\begin{cases}
左右に存在 & result < 0 \\
片方に存在 & result > 0 \\
重複? & result = 0
\end{cases}
\]
外積計算
\[
\begin{aligned}
|a\times b| &= |a||b|sin\theta \\
\\
a\times b&=
\begin{pmatrix}
a_2b_3-a_3b_2 \\
a_3b_1-a_1b_3 \\
a_1b_2-a_2b_1
\end{pmatrix}
\end{aligned}
\]
2Dに限ると
\[
|a\times b| = (a_x b_y )-(a_yb_x)
\]
Reference
最終更新日:
August 14, 2023
作成日: August 14, 2023
作成日: August 14, 2023