座標変換
2次元
- 2次元直交座標系 $$ (x,y) $$
- 極座標系
$$
\begin{cases}
x = rcos\theta
\\
y = rsin\theta
\end{cases}
$$
\(r\): 半径
\(\theta\): 角度
スキュー(せん断)
-
x方向
\(\alpha\): y軸からの差分角度(x軸と平行な辺をずらした量)\[ \begin{aligned} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & tan\alpha & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{aligned} \] -
y方向
\(\beta\): x軸からの差分角度(y軸と平行な辺をずらした量)\[ \begin{aligned} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ tan\beta & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{aligned} \]
3次元
- 円柱座標系
- hogehoge
-
極座標系 $$ \begin{cases} x = rsin\theta cos\phi \\ y = rsin\theta sin\phi \\ z = rcos\theta \end{cases} $$
- \(\phi\): \(0\sim 2\pi\)
x-y平面での角度(x軸原点) - \(\theta\): \(0\sim \pi\)
z軸からx-y平面へのの角度(z軸原点)
- \(\phi\): \(0\sim 2\pi\)
-
左手系
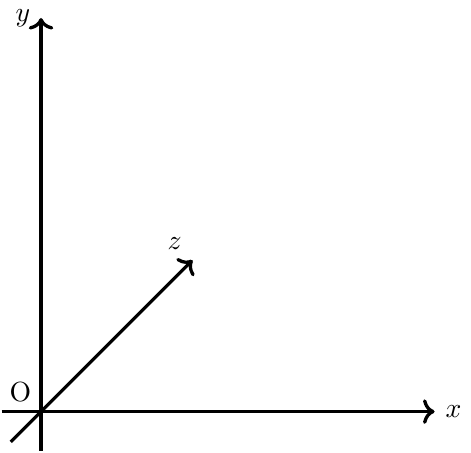
- 右手系
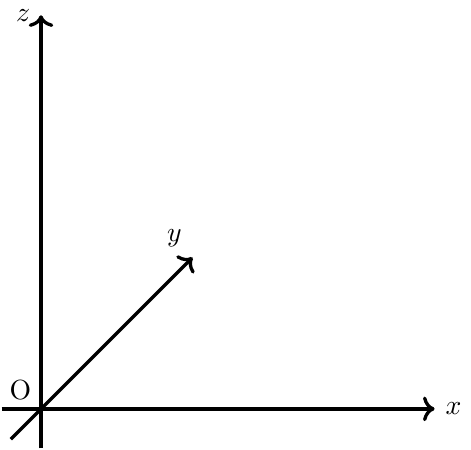
平行移動
\[
\begin{aligned}
\underset{result}{
\begin{pmatrix}
x'\\
y'\\
z'\\
1
\end{pmatrix}
}
&=
\begin{pmatrix}
1 & 0 & 0 & t_x \\
0 & 1 & 0 & t_y \\
0 & 0 & 1 & t_z \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}
\\
&=T(t_x, t_y, t_z)
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}
\end{aligned}
\]
拡大・縮小
\[
\begin{aligned}
\begin{pmatrix}
x' \\ y' \\ z' \\ 1
\end{pmatrix}
&=
\begin{pmatrix}
s_x & 0 & 0 & 0 \\
0 & s_y & 0 & 0 \\
0 & 0 & s_z & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}
\\
&=
S(s_x, s_y, s_z)
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}
\end{aligned}
\]
回転
x軸
\[
\begin{aligned}
\begin{pmatrix}
x' \\ y' \\ z' \\ 1
\end{pmatrix}
&=
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & cos\theta & -sin\theta & 0 \\
0 & sin\theta & cos\theta & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}
\\
&=
R_x(\theta)
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}
\end{aligned}
\]
y軸
\[
\begin{aligned}
\begin{pmatrix}
x' \\ y' \\ z' \\ 1
\end{pmatrix}
&=
\begin{pmatrix}
cos\theta & 0 & sin\theta & 0 \\
0 & 1 & 0 & 0 \\
-sin\theta & 0 & cos\theta & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}
\\
&=
R_y(\theta)
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}
\end{aligned}
\]
z軸
\[
\begin{aligned}
\begin{pmatrix}
x' \\ y' \\ z' \\ 1
\end{pmatrix}
&=
\begin{pmatrix}
cos\theta & -sin\theta & 0 & 0 \\
sin\theta & cos\theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}
\\
&=
R_z(\theta)
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}
\end{aligned}
\]
鏡映
xy平面に関する鏡映(z軸反転)
\[
\begin{aligned}
\begin{pmatrix}
x' \\ y' \\ z' \\ 1
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
x \\ y \\ z \\ 1
\end{pmatrix}
\end{aligned}
\]
Reference
最終更新日:
August 14, 2023
作成日: August 14, 2023
作成日: August 14, 2023